In this article, we describe the two types of coordinate systems used in a plane: the Cartesian coordinate system and the polar coordinate system. These coordinate systems are utilized by our graphing calculator.
Assuming you are familiar with one-dimensional coordinate systems, also called a number line or axis, we will focus on two-dimensional coordinate systems. A two-dimensional coordinate system, also known as a coordinate plane, is used to locate an ordered pair (a,b) in a plane.
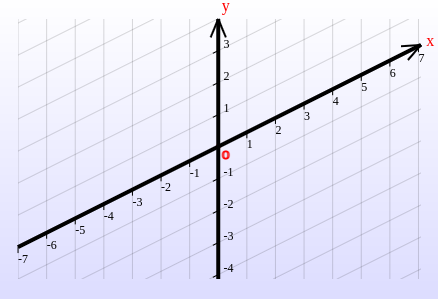
The Cartesian coordinate system is formed by two intersecting axes with a common
origin. The axis containing the values of the first coordinate is usually drawn horizontally,
while the other is drawn vertically. These axes are commonly denoted by the letters x and y and are called the
x-axis and y-axis, respectively.
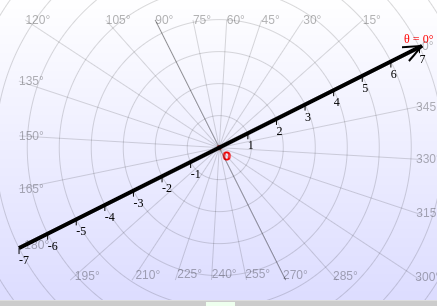
On the other hand, the polar coordinate system uses one reference axis, usually horizontal, called the polar axis. Its origin is called the pole. Unlike the Cartesian coordinate system which uses a second axis, the polar coordinate system uses angles measured from the polar axis about the pole.
The following figures illustrate the Cartesian coordinate system and the polar coordinate system used in a plane.
The Cartesian coordinate system uses a horizontal axis and a vertical axis to locate points in a plane.
The polar coordinate system uses a distance from the origin and an angle from a reference direction to locate points in a plane.
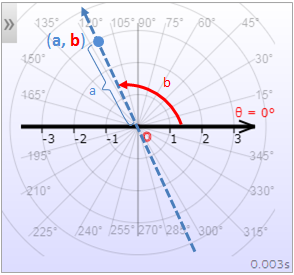
Both the Cartesian coordinate system and polar coordinate system can be used to locate or plot points. By plotting points one can plot the graph of functions, and graph of parametric equations. The following figures illustrate how the point (a,b) is plotted in each coordinate system for a=3 and b=2.
a=3, b=2
a=3, b=2 (≃115°)
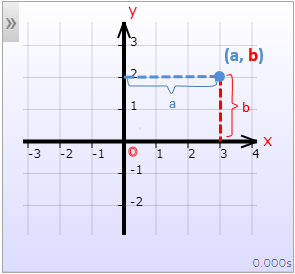
In the Cartesian coordinate system with the x-axis and y-axis as previously described, the first coordinate, a, is referred to as the (or abscissa) while the second coordinate, b, is called the y-coordinate (or ordinate).
In the polar coordinate system, a is referred to as the radial coordinate, while b is known as the angular coordinate or polar angle. The radial coordinate represents the signed distance from the pole, while the angular coordinate represents the angle by which the polar axis must be rotated counterclockwise to locate the point (a,b).
In the Cartesian coordinate system, the point (a,b) can be described as x = a and y = b. In the polar coordinate system, it is customary to use r and θ (or φ) to represent the point, where r = a and θ = b (or φ = b).
Every ordered pair (a,b) has a unique location in a coordinate plane. However, a location (point) in the polar coordinate system can have multiple polar representations. This is because adding multiples of 2π (or 360°) to an angle does not change its "location". Therefore, the ordered pairs (a,b+2π) and (a,b) determine the same point in the polar coordinate plane. Similarly, adding π to the angular coordinate and changing the radial coordinate from a to -a also determines the same point as (a,b), as shown in the following illustrations:
a,b + 2π)
-a,b + π)
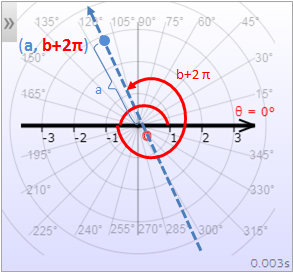
In summary, all the ordered pairs (a,b), (a,b+2nπ) and (-a,b+(2n+1)π) identify the same point in the polar coordinate system for integers n.
Learn how to convert between Cartesian and polar Coordinates.
If the axes are perpendicular, as shown above, the Cartesian coordinate system in a plane is called the rectangular coordinate system or orthogonal coordinate system. However, the axes need not be perpendicular, in which case, we have an oblique coordinate system or non-orthogonal coordinate system, as demonstrated in the following figures. Note that the polar axis in the polar coordinate system need not be horizontal either.
