Skew (Oblique) Coordinate Systems: Cartesian and Polar

In this article, we introduce skew (also known as slanted or oblique) coordinate systems. These are generalizations of rectangular and polar coordinate systems, typically obtained by rotating one or both of the axes. We also introduce our suite of tools—including our proprietary graphing calculator—which are the world’s only graphing tools capable of plotting in skew coordinate systems.

Skew (Oblique) Cartesian Coordinate Systems

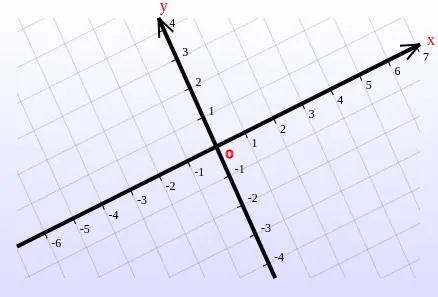
The standard Cartesian coordinate system, often called the rectangular coordinate system, utilizes two perpendicular axes: one horizontal and one vertical. By rotating either of these axes independently, we create a Cartesian coordinate system where the axes intersect at an arbitrary angle rather than a fixed 90 degrees. This is known as a skew Cartesian coordinate system (or oblique Cartesian coordinate system), as demonstrated in Fig 1, which stands in contrast to the rectangular coordinate system shown in Fig 2.

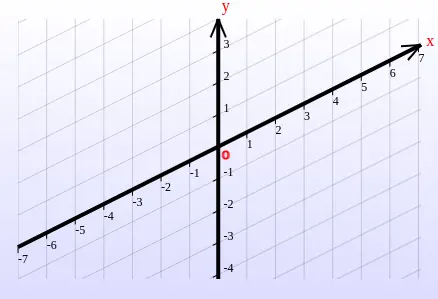
An oblique Cartesian coordinate system where the y-axis is vertical but the x-axis is rotated upward, creating a parallelogrammic grid with non-perpendicular intersections. — *Fig 1.* **Skew Cartesian Coordinate System:** The independent x-axis is rotated, causing the grid lines to form **parallelograms**.

A standard rectangular Cartesian coordinate system showing two perpendicular axes, x (horizontal) and y (vertical). — *Fig 2.* **Rectangular Cartesian Coordinate System:** The axes remain perpendicular, and the grid lines form **rectangles**.

Our skew graphing calculator and other skew graphers are the only graphing tools that allow you to rotate axes and plot within skew Cartesian coordinate systems. This offers an interactive way to explore and master graphing in more generalized coordinate environments. While many texts use "Cartesian coordinate system" and "rectangular coordinate system" interchangeably, we prefer the more precise term rectangular Cartesian coordinate system to distinguish it from the skew Cartesian coordinate systems introduced here.

In the context of Cartesian coordinates, skew coordinate systems are types of parallelogrammic coordinate systems. This naming is due to the parallelograms formed by grid lines, which remain parallel to the corresponding axes. Following the same logic that all rectangles are also parallelograms, rectangular coordinate systems are also parallelogrammic coordinate systems.

Remark: It is important to note that when both axes are rotated by the same angle—preserving their perpendicularity, as shown in Fig 3—the system remains rectangular. It does not become "skew," even though the axes are tilted relative to the standard horizontal and vertical orientations.

A Cartesian coordinate system where both axes are rotated by the same angle; the grid remains rectangular but is tilted relative to the horizon. — *Fig 3.* **Rotated Rectangular System:** Both axes are rotated by the same angle, preserving their **perpendicularity**.

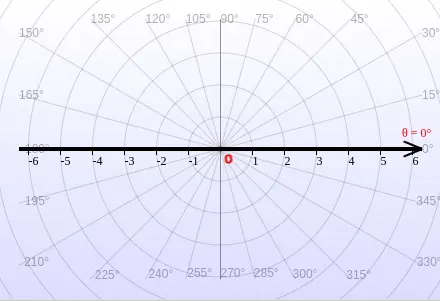
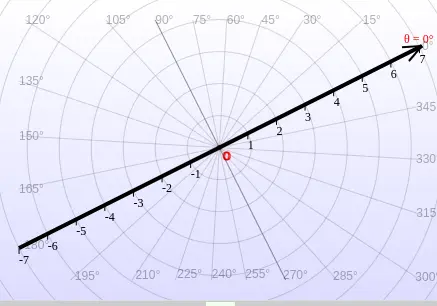
Skew Polar Coordinate Systems

In the standard polar coordinate system (Fig 4), the polar axis is traditionally fixed horizontally, extending to the right from the pole (origin). However, our polar graphing calculator and other polar graphers allow you to redefine this reference by rotating the polar axis to any arbitrary angle. This flexibility allows you to plot points, functions, and complex mathematical expressions in a skew polar coordinate system.

A standard polar coordinate system showing a horizontal polar axis (0 degrees) with concentric circular grid lines and radial lines extending from the origin. — *Fig 4.* **Standard Polar Coordinate System:** The polar axis is drawn **horizontally**.

A skew (oblique) polar coordinate system where the polar axis is tilted from the horizontal position, with the radial grid lines rotated accordingly. — *Fig 5.* **Skew Polar Coordinate System:** The polar axis is rotated, establishing a **new angular baseline** for the entire coordinate frame.