
A complex number in rectangular (standard) form a+bi can be expressed in phasor (polar) form r∠φ (and vice versa). Here r is known as the length (or magnitude), and φ is referred to as the phasor (or argument) of the complex number, which is the angle that the vector (a,b) makes with the positive real axis. Our Complex Number Calculator utilizes the following formulas to convert between these two forms.
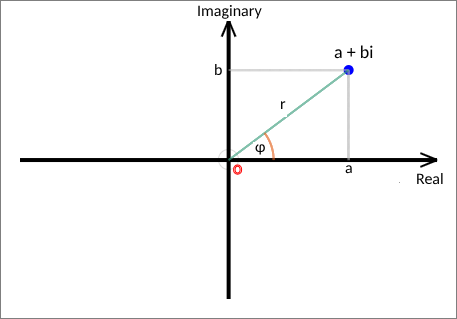
As shown in the following figure, regardless of the location of the point a+bi, we have, by the Pythagorean Theorem r =√(a2 + b2)
We also have tan(φ) = b/a
By definition of tan-1, we have φ = tan-1(b/a) if a+bi is in the first or fourth quadrant (where a > 0), as tan-1 always gives an angle between -π/2 and π/2.
Note that the above also holds for a = 0, which implies r = |b|, and φ = ±π/2 depending on the sign of b.
If a+bi is in the second or third quadrant (where a < 0), we must add or subtract π to tan-1(b/a) to obtain the correct angle.
To summarize:
Rectangular to Phasor/Polar Form
For a complex number with rectangular form a+bi, the phasor/polar form is:
r∠φ, where
In the trivial case where both a and b are 0, we get r = 0, and φ can be any number, such as 0.
Note that φ is not unique; they all differ by an integer multiple of 2π.
Converting a polar form to rectangular form is straightforward using the definitions of trigonometric functions on a trigonometric circle. Referring to the above figure, we have a = rcos(φ) and b = rsin(φ).
So we have the following formula for converting polar coordinates to Cartesian coordinates:
Polar (Phasor) to Cartesian (Rectangular) Form
For a complex number in phasor/polar form r∠φ, the rectangular form is:
Note: The above conversion formula holds even if r is negative: If r < 0, then a = -|r|*cosφ = -(-r)*cosφ = r*cosφ, and similarly, b = -|r|*sinφ = -(-r)*sinφ = r*sinφ.